Teoría Unidad 1
ver
Magnitudes Físicas - Factores de conversión
Cuestionario TP N°1
Apunte clases Unidad 1- Descargar PDF
Teoría Unidad 1: LEYES DE NEWTON
Definición de Masa y Peso
Puedes leer mas Aquí
Ver Video sobre el cocepto de Masa
Puedes ver información de los Planetas Aquí
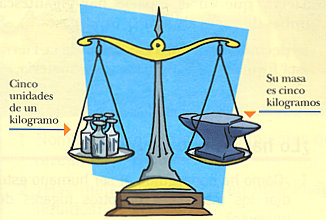
Masa o peso...¿qué se mide cuando "se pesa en kg con una balanza"?
En realidad medimos la masa en kg.
En realidad medimos la masa en kg.
Todos los cuerpos están hechos de materia. Algunos tienen más materia que otros. Por ejemplo, pensemos en dos pelotas de igual tamaño (igual volumen): una de golf (hecha de un material duro como el caucho) y otra de tenis (hecha de goma, más blanda).
Aunque se vean casi del mismo tamaño, una (la de golf) tiene más materia que la otra.
Como la masa es la cantidad de materia de los cuerpos , diremos que la pelota de golf tiene más masa que la de tenis.
Lo mismo ocurre con una pluma de acero y una pluma natural. Aunque sean iguales, la pluma de acero tiene más masa que la otra.
Puedes leer mas Aquí
Masa de un cuerpo
Materia: se llama materia a todas las partículas que forman a un cuerpo. Por ejemplo: un pedazo de madera, el agua dentro de un recipiente, etc.
Todo elemento químico que existe en la naturaleza se llama átomo, y tiene masa y peso, por ejemplo el oro, el hierro, el cobre, el calcio, etc. Estos elementos de la naturaleza se los representan y clasifican en la tabla periódica de los elementos químicos.
En química una molécula de agua se la representa con la fórmula: HO₂, quiere decir que una molécula de agua, está formada por un átomo de Hidrógeno y dos átomos de Oxigeno. Imagínense el mar que está formado por millones y millones de moléculas de agua.
Entonces podemos decir que:
“Llamaos Masa de un cuerpo, a la cantidad de materia que posee un cuerpo”.
“Llamaos Masa de un cuerpo, a la cantidad de materia que posee un cuerpo”.
La masa se mide en kg
¿Qué se mide cuando se usa una balanza?
Es común que en nuestras vidas desde niños, usemos erróneamente el concepto de Peso y usemos la unidad de medida kg, y en realidad, lo que se está midiendo es la masa del cuerpo en kg.
El kg es por tanto una unidad de masa, no de peso. Sin embargo, muchos aparatos utilizados para medir pesos (básculas, por ejemplo), tienen sus escalas graduadas en kg en lugar de kg-fuerza. Esto no suele representar, normalmente, ningún problema ya que 1 kg-fuerza es el peso en la superficie de la Tierra de un objeto de 1 kg de masa. Por lo tanto, una persona de 60 kg de masa pesa en la superficie de la Tierra 60 kg-Fuerza. Sin embargo, la misma persona en la Luna pesaría solo 10 kg-fuerza, aunque su masa seguiría siendo de 60 kg. (El peso de un objeto en la Luna, representa la fuerza con que ésta lo atrae)
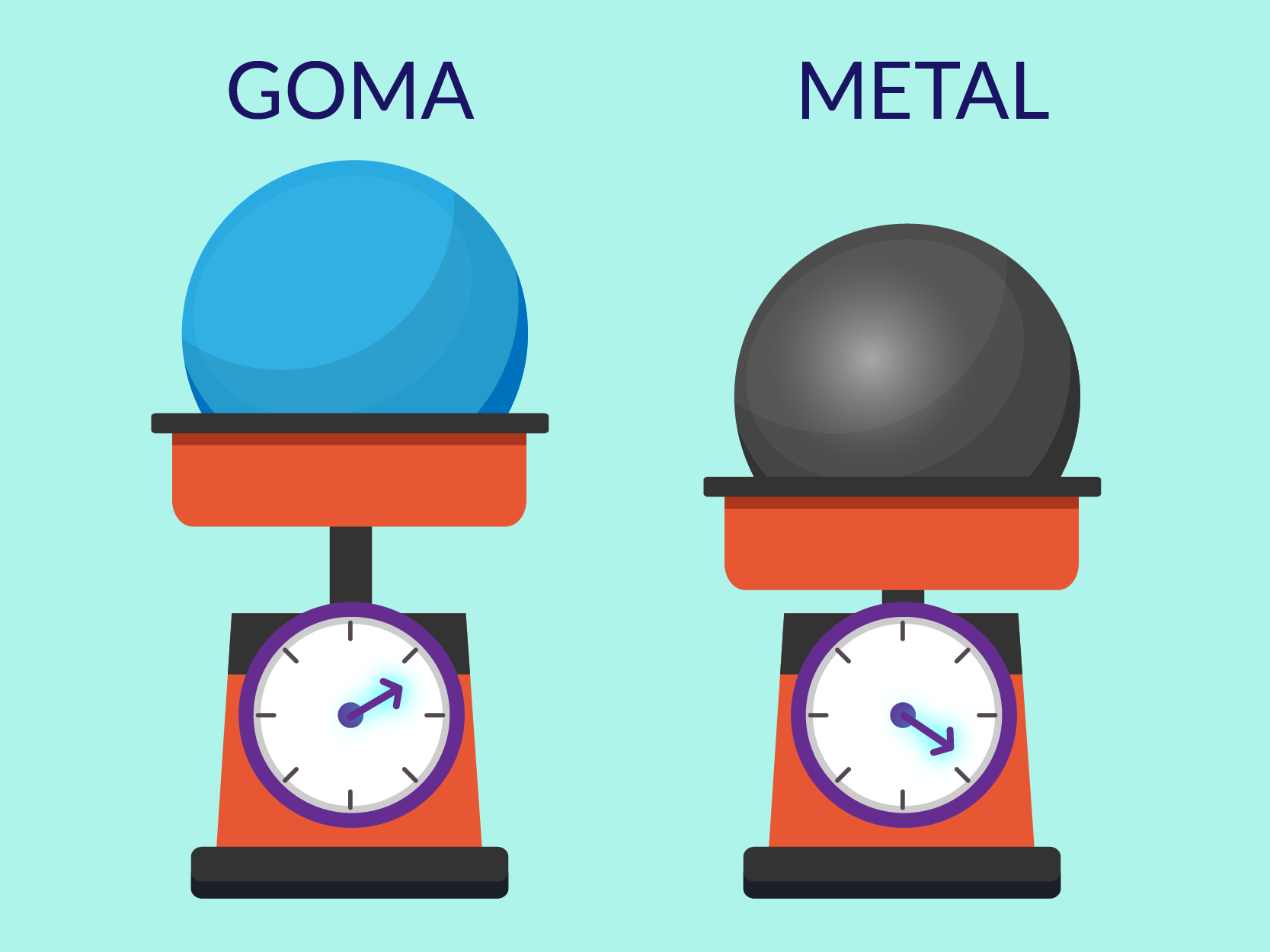
Si ponemos en dos básculas iguales 1 kg de plomo y 1 kg de paja, ¿marcarán lo mismo?
Como hemos visto en la pregunta anterior , 1 kg de plomo y 1 kg de paja pesan lo mismo : 1 kg-fuerza. Parece por tanto que las dos básculas deberían de marcar igual. Sin embargo no es así, ya que una báscula no indica el peso del objeto que se coloca encima, sino la fuerza que él mismo hace sobre ella. ¿Qué marcaría la báscula si colocásemos sobre ella un globo de feria. Evidentemente y a pesar de tener peso (la Tierra lo atrae como a todos los objetos que tienen masa), la báscula no marcaría nada, porque el globo se iría volando y no haría ninguna fuerza sobre ella.
El plomo y la paja, no hacen la misma fuerza sobre la báscula aunque su peso sea igual. Esto se debe a que el aire los empuja hacia arriba con una fuerza distinta.
El aire, como todos los fluidos (gases y líquidos), ejerce una fuerza hacia arriba, denominada empuje, sobre los cuerpos que se encuentran en su interior. Esta fuerza es tanto mayor, cuanto mayor sea el volumen del cuerpo.
Como 1 kg de paja tiene un volumen mucho mayor que 1 kg de plomo, el empuje del aire sobre la paja es también mucho mayor que sobre el plomo.
La báscula que tiene la paja, marcará por tanto un poco menos.
La diferencia es pequeña, aproximadamente 1 g-fuerza.
Ver Video sobre el cocepto de Masa
Tabla masa del Sol y los planetas:
Planeta o cuerpo Celeste
|
Masa (kg)
| |
Luna
|
7.35 x 10²²
| |
Sol
|
1.9891 x 1030
| |
Júpiter
|
0.3302 x 1024
| |
Saturno
|
4.8685 x 1024
| |
Neptuno
|
5.9736 x 1024
| |
Urano
|
0.6418 x 1024
| |
Tierra
|
1898.6 x 1024
| |
Venus
|
568.46 x 1024
| |
Marte
|
86.810 x 1024
| |
Mercurio
|
102.43 x 1024
|
Ver Datos en Wikipedia Aqui
El Peso de un cuerpo es la Fuerza con que lo atrae la Tierra y depende de la masa del mismo. Un cuerpo de masa el doble que otro, pesa también el doble. Se mide en Newtons (N) y también en kg-fuerza, dinas, libras-fuerza, onzas-fuerza, etc.
En consecuencia de lo anterior podemos decir que:
Ejemplo 1: Calcular la masa de un cuerpo en la tierra que tiene 500 N (Newton) de Peso.
En la tierra g= 9,8 m/seg²
Solución:
Usamos la fórmula del peso P = m * g
Despejando la masa "m" quedaría: m = P
g
m = 500 N
9,8 m/seg²
El resultado es:
m = 51,2 kg
Siempre debes tener presente las unidades de medidas de cada magnitud
Cuando hablamos de Peso, también hablamos de Fuerza, que significan lo mismo, según Sistema internacional de medidas (SI).
Formulas para calcular el Peso:
P = m * g
Donde:
P: Peso en Newton
m: Masa en kg
g: aceleración de la gravedad en m/seg²
También en la segunda Ley de Newton el peso se calcula:
P = m * a
Donde:
P: Peso en Newton [N]
m: Masa en kg
a: aceleración en m/seg² (aceleración de un objeto que se mueve sobre la tierra).
La masa también se puede calcular en función de la densidad y el volumen
m = ρ * v
Donde:
También podemos calcular el densidad como el peso especifico dividida por la aceleración de la gravedad.
ρ = Pe
g
Donde: Pe = Peso específico [N/m3]
ρ = Densidad [kg/m3]
g = Aceleración de la gravedad [m/s2]
Fuerzas
Llamaos Fuerza a todo aquello que tiende a modificar el estado d reposo o de movimiento de un cuerpo, por ejemplo empujar un automóvil o detenerlo.
Cuando sostenemos un cuerpo o tratamos de levantarlo, el esfuerzo muscular nos da la idea de Fuerza, y a la vez, de una magnitud de ese peso que llamamos Peso.
Si suspendemos un objeto cualquiera suspendido por medio de un hilo (ver figura), se siente que el hilo se pone tenso, y si se llegara a cortar, el cuerpo se caería hacia el suelo.
Este fenómeno se produce por la acción de la Fuerza actúa sobre todos los cuerpos ubicados en la superficie terrestre y se llama Fuerza de Gravedad.
La fuerza de gravedad
La fuerza de la gravedad también llamada aceleración de la gravedad, tiene sentido hacia el centro de la Tierra, se la representa con la letra “g”, la misma depende de la masa de un cuerpo, de la cantidad de materia que tiene un cuerpo, esto es significativo cuando tienen grandes cantidades de masa como como por ejemplo: la Luna, la tierra, el sol, etc. Cuando más Masa tiene un cuerpo mayor es la fuerza de atracción.
El valor de la fuerza de la gravedad g, en la tierra es 9,8 en el nivel del mar, en el paralelo del Ecuador (máxima circunferencia de la tierra que pasa por Ecuador), y se mide en m/seg².
g = 9,8 m/seg²
La fuerza o aceleración de la gravedad no es la misma en todos los puntos de la tierra, porque la tierra no tiene el mismo diámetro en todos sus puntos. Se ha podido comprobar que es mayor en los polos como se puede ver en la figura.
En consecuencia de lo anterior podemos decir que:
“El peso de un cuerpo representa la fuerza de gravedad que se ejerce sobre él”.
Si colgásemos varios cuerpos distintos, en varios resortes iguales (ver figura), se puede ver que se producen distintos estiramientos, por lo cual podemos decir que tienen distinto peso.
Si en cambio en una nueva medición, los estiramientos son iguales como se puede ver en la siguiente figura, se puede decir que los cuerpos tienen el mismo peso.
En todos los casos los estiramientos se han producido por acción de la fuerza de la gravedad sobre esos cuerpos.
Por ello podemos decir que:
“Peso de un cuerpo es la mayor o menor “Fuerza” de atracción de la gravedad que la tierra ejerce sobre un cuerpo situado sobre ella”.
En Física el peso de un cuerpo se calcula como el producto de la masa m (kg) por la aceleración de la gravedad g (m/seg²),según SI y SIMELA ver tema LINK:
P = m * g
Donde
P: Peso del cuerpo en N (Newton)
m: masa del cuerpo en kg
g: aceleración de la gravedad de la tierra, g= 9,8 m/seg² (al nivel del mar en el paralelo Ecuador)
Unidad de medida: La Fuerza o el Peso se miden Newton (N). Link Aclaración, historia del peso, la masa simela, SI.
De la fórmula: P = m * g [N] = [kg]*[m/seg²]

Ejemplo 1: Calcular el peso de un cuerpo en la tierra que tiene 50 kg de masa.
En la tierra g= 9,8 m/seg²
Solución:
Usamos la fórmula del peso P = m * g
P = 50 kg * 9,8 m/seg²
El resultado es:
P = 490 N (Newton)

Ejemplo 1: Calcular el peso de un cuerpo en la tierra que tiene 50 kg de masa.
En la tierra g= 9,8 m/seg²
Solución:
Usamos la fórmula del peso P = m * g
P = 50 kg * 9,8 m/seg²
El resultado es:
P = 490 N (Newton)
Ejemplo 1: Calcular la masa de un cuerpo en la tierra que tiene 500 N (Newton) de Peso.
En la tierra g= 9,8 m/seg²
Solución:
Usamos la fórmula del peso P = m * g
Despejando la masa "m" quedaría: m = P
g
m = 500 N
9,8 m/seg²
El resultado es:
m = 51,2 kg
Siempre debes tener presente las unidades de medidas de cada magnitud
Cuando hablamos de Peso, también hablamos de Fuerza, que significan lo mismo, según Sistema internacional de medidas (SI).
Por lo que también podemos expresar la medida del peso P como la fuerza F:
F = m * g
Donde
P: Peso del cuerpo en Newton
m: masa del cuerpo en kg
g: aceleración de la gravedad de la tierra, g= 9,8 m/seg² (al nivel del mar en el paralelo Ecuador)
Ejemplo 1: Calcular la fuerza F que ejerce un cuerpo sobre la tierra que tiene 100 kg de masa.
En la tierra g= 9,8 m/seg²
Solución:
Usamos la fórmula del peso F = m * g
F = 100 kg * 9,8 m/seg²
El resultado es:
F = 500 N (Newton)
Por lo que podemos enunciar que:
“El Peso de un cuerpo de un cuerpo varía con la latitud del lugar: su valor máximo lo adquiere en los polos, y disminuye hacia el Ecuador, logrando allí su valor mínimo”.
El Peso de un cuerpo también varía con la altura
Imagina el mismo cuerpo en el resorte, pero colocado a cierta altura sobre el nivel del mar, por ejemplo un avión a mil, dos mil o más metros de altura, Sucede que al estar más alejado del suelo de la tierra, la acción de la fuerza gravitatoria disminuye a medida que aleja, y por lo tanto su peso también disminuye como se puede apreciar e la figura.
En consecuencia podemos decir que:
“El peso de un cuerpo varia en proporción inversa a la distancia respecto a la tierra”. O bien “A medida que se aleja el cuerpo de la tierra, este pesa menos, y si saliera al espacio este flotaría y orbitaría sobre la tierra como lo hace la Luna alrededor de la tierra, o como la tierra orbita alrededor del Sol”.
Formulas para calcular el Peso:
P = m * g
Donde:
P: Peso en Newton
m: Masa en kg
g: aceleración de la gravedad en m/seg²
También en la segunda Ley de Newton el peso se calcula:
P = m * a
Donde:
P: Peso en Newton [N]
m: Masa en kg
a: aceleración en m/seg² (aceleración de un objeto que se mueve sobre la tierra).
La masa también se puede calcular en función de la densidad y el volumen
m = ρ * v
Donde:
ρ = Densidad [kg/m3], también se la representa con la letra "d".
m = Masa [kg]
v = Volumen [m3]
También podemos calcular el densidad como el peso especifico dividida por la aceleración de la gravedad.
ρ = Pe
g
Donde: Pe = Peso específico [N/m3]
ρ = Densidad [kg/m3]
Pe = ρ
V
Donde:
Donde:
V
Donde:
Pe = Peso específico [N/m3]
ρ = Densidad [kg/m3]
v = Volumen [m3]
También podemos calcular el peso específico como la densidad multiplicada por la aceleración de la gravedad.
Pe = ρ * g
Donde:
Pe = Peso específico [N/m3]
ρ = Densidad [kg/m3]
g = Aceleración de la gravedad [m/s2]
Para pensar:
¿Qué piensas, Es lo mismo decir Peso y Fuerza? ¿Representan el mismo concepto?
¿Es lo mismo Peso y Masa? ¿Representan el mismo concepto?
¿Qué piensas, Es lo mismo decir Peso y Fuerza? ¿Representan el mismo concepto?
¿Es lo mismo Peso y Masa? ¿Representan el mismo concepto?
Unidades de medida de la masa y el peso en los distintos sistemas de medida
Magnitudes
|
Sistema Absoluto
|
Sistema Técnico
| |||
SI - M.K.S
|
C.G.S
|
F.P.S
|
Europeo
|
Inglés
| |
Masa
|
Kg
|
g
|
lb
|
UTM
|
slug
|
Peso o Fuerza
|
N = Kg.m/s2
|
Dina = g.cm/s2
|
Poundal = lb.pie/s2
|
kg.f
|
lb.f
|
Aceleración
|
m/s2
|
cm/s2
|
pie/s2
|
m/s2
|
pie/s2
|
Puedes ver mas sobre los distintos sistemas de medida aquí
Te invito a que veas los siguientes videos de Youtube sobre masa y peso:
Video 1
|
Video 2 Link
|
Diferencia entre masa y peso
Características de masa
|
|
Características de peso
|
|
Ley de Gravitación universal
Los primeros esfuerzos de Newton en comprender el movimiento de los cuerpos celestes los dirigió hacia la Luna. Por sus conocimientos acerca del movimiento de los cuerpos en la Tierra sabía que si la Luna no se movía en línea recta y con velocidad constante era porque sobre ella se ejercía una fuerza que era la causa de que el satélite curvara su trayectoria. ¿Cuál es la fuerza que hace que la Luna se mueva alrededor de la Tierra?
Cuentan que Newton dijo que la respuesta a esta interrogante la encontró un día que meditaba sentado en el jardín y una manzana cayó al suelo; entonces pensó, que la fuerza que la Tierra ejercía sobre la manzana, también podía ejercerse sobre la Luna. ¿Serán correctas las suposiciones de este eminente científico?
¿Qué es la Ley de Gravitación Universal?
La Ley de Gravitación Universal es una de las leyes físicas formuladas por Isaac Newton en su libro Philosophiae Naturalis Principia Matemática de 1687.
Describe como la interacción gravitatoria entre cuerpos dotados de masa, y establece una relación proporcional de la fuerza con que esos cuerpos se atraen el uno al otro.
Para formular esta ley, Newton dedujo que la fuerza con que dos masas se atraen es proporcional al producto de sus masas dividido entre a distancia que los separa al cuadrado.
Enunciado de la Ley de Gravitación Universal
El enunciado formal de esta ley newtoniana dice que:
“La fuerza con que se atraen dos objetos es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa”.
Esto significa que dos cuerpos cualquiera se atraen con una fuerza mayor o menor según su masa sea mayor o menor, y según la distancia entre ellos también lo sea.
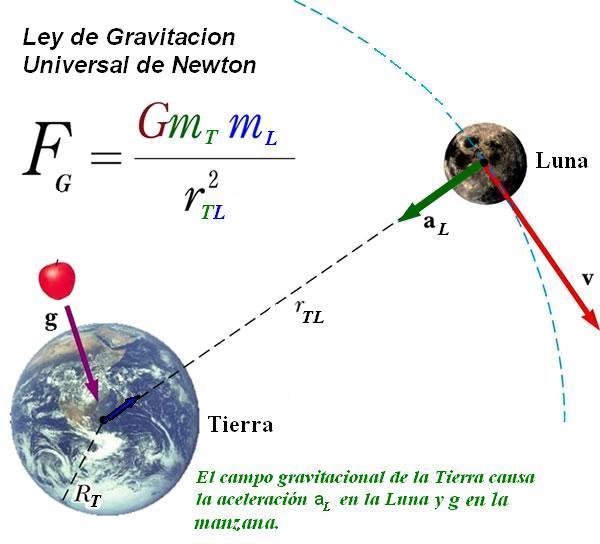
Fórmula de la Ley de Gravitación Universal
La fórmula fundamental de la Ley de Gravitación Universal es la siguiente:
F = G * m₁ * m₂
r²
En donde:
F es la fuerza de atracción entre dos masas
G es la constante de gravitación universal (calculada en 6,673484 * 10e11 N.m²/kg²)
kg²
m₁ es la masa del primer cuerpo
m₂ es la masa del segundo cuerpo
La intensidad de la fuerza gravitacional varía proporcionalmente con la masa de los cuerpos. Para cuerpos de grandes masa esta fuerza es significativa, por ejemplo, entre el Sol y la Tierra, entre la Tierra y la Luna, en las interacciones entre galaxias y estrellas. En la superficie de la Tierra, la atracción gravitacional entre los cuerpos no es percibida, porque las masas son muy pequeñas si se comparan con la de los cuerpos celestes, por tal razón la noción de gravedad es asociada solamente a la Tierra y no a los cuerpos que en ella se encuentran. Para distancias pequeñas la fuerza aumenta, pero a distancias atómicas prevalecen otras fuerzas.entre otros.
Te invito a que ves el siguiente video de Youtube
Ley de Gravitación universal: incluye 1°, 2° y 3° ley de Kepler
Simulador de Fuerza Gravitacional
ver el siguiente Simulador prueba y comenta la experiencia aquí (obligatorio)
Modifica las variables que allí aparecen, registra los cambios y extrae conclusiones.
ver también el siguiente Simulador prueba y y comenta la experiencia aquí (obligatorio)
Aceleración de la Gravedad "g" en la Tierra
Según las leyes de Newton toda fuerza ejercida sobre un cuerpo imprime a éste una aceleración. En presencia de un campo gravitatorio todo cuerpo se ve sometido a la fuerza de la gravedad, y la aceleración que esta fuerza imprime se conoce como aceleración de la gravedad y se representa por la letra g. De este modo, todo cuerpo que se somete a la libre influencia del campo gravitatorio (es decir, sin otras fuerzas que interfieran, como el rozamiento) caerá con una velocidad creciente.
El valor de g depende de la fuerza gravitatoria en cada punto del campo, y coincide con la intensidad del campo gravitatorio en dicho punto. En la superficie de la Tierra g tiene un valor de 9,8 m/seg2. Este valor de g es considerado como el valor de referencia, y así se habla de naves o vehículos que aceleran a varios g. En virtud del principio de equivalencia, un cuerpo bajo una aceleración dada sufre los mismos efectos que si estuviese sometido a un campo gravitatorio cuya aceleración gravitatoria fuese la misma.
Valor de g para la tierra:
g= 9,8 m/s²
También Puedes ver mas aquí
Si en la tierra al nivel de mar g vale 9,8 m/s².
¿Qué opinas?
- ¿Si cavamos un pozo y nos dirigimos hacia el centro, el valor de g aumenta o disminuye?
- ¿Si subimos a las cordillera de los andes o al Himaya, el valor de g aumenta o disminuye?
Gravedad en otros Planetas y cuerpos celestes
Planeta o cuerpo Celeste
|
Gravedad (m/seg²)
| |
Luna
|
1.6
| |
Sol
|
274
| |
Júpiter
|
23,12
| |
Saturno
|
8,96
| |
Neptuno
|
11
| |
Urano
|
8,69
| |
Tierra
|
9,8
| |
Venus
|
8,87
| |
Marte
|
3,71
| |
Mercurio
|
3,70
|
¿Quieres saber cuanto pesarías en otros Planetas? Entra aquí
Leyes de Newton
Las leyes de Newton marcaron una revolución dentro del campo de la física. Constituyeron los cimientos de la dinámica (parte de la mecánica que estudia el movimiento según las fuerzas que lo originan). Además, al combinar estos principios con la ley de la gravitación universal, se pudieron explicar las leyes del astrónomo y matemático alemán, Johannes Kepler, sobre el movimiento de los planetas y satélites. (ver ejemplos aqui)
1° Ley de Newton
La primera ley de Newton, conocida también como Ley de inercia, nos dice que si sobre un cuerpo no actúa ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero).
Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento. La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actua ninguna fuerza neta se mueve con velocidad constante.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
Ver video aquí
Ejemplos, ejercicios.
2° Ley de Newton
La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera: F = m a
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:
F = m a
Donde:
F: Fuerza medida en Newton [N]
m: masa del cuerpo, medida en [kg]
a: Aceleración del cuerpo, medida en [m/seg2]
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea:
F: Fuerza medida en Newton [N]
m: masa del cuerpo, medida en [kg]
a: Aceleración del cuerpo, medida en [m/seg2]
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea:
1 N = 1 Kg · 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m · a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.
Ver Video aquí
Ver Ejemplos, ejercicios.
Más videos con Peso, Masa y Gravedad aquí
3° Ley de Newton
Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.
La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros también nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actúan sobre cuerpos distintos.
Ver video aquí
Ver Ejemplos
Te invito a ver los siguientes videos de Youtube sobre las leyes de newton
¿Cómo funcionan las leyes de Newton?
Te invito a que materialices los conceptos de la leyes de newton usando los siguientes simuladores:
- visita este sitio y prueba los simuladores Simuladores
- Simulador Fuerza de Gravedad
- Simulador 1° Ley de Newton
- Simulador 2° Ley de Newton
- Simulador 3° Ley de Newton
Aprende Más con videos que te van a interesar
Si te interesan estos conceptos de Física, te recomiendo veas el siguiente video que incluye lo anterior y las teorías de Albert Einstein
Mas de Albert Einstein:
ver
Magnitudes Físicas - Factores de conversión
Cuestionario TP N°1
Apunte clases Unidad 1- Descargar PDF



















Comentarios
Publicar un comentario